Mitchell's embedding theorem
Mitchell's embedding theorem, also known as the Freyd–Mitchell theorem, is a result stating that every abelian category admits a full and exact embedding into the category of R-modules. This allows one to use element-wise diagram chasing proofs in arbitrary abelian categories.
Applications
Using the theorem we can treat every abelian category as if it is the category of R-modules concerning theorems about existence of morphisms in a diagram and commutativity and exactness of diagrams. Category theory gets much more concrete by this embedding theorem.
Sketch of the proof
First we construct an embedding from an abelian category 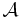 to the category
to the category 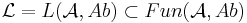 of left exact functors from the abelian category
of left exact functors from the abelian category 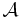 to the category of abelian groups
to the category of abelian groups 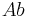 through the functor
through the functor  by
by 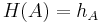 for all
for all 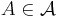 , where
, where 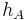 is the covariant hom-functor. The Yoneda Lemma states that
is the covariant hom-functor. The Yoneda Lemma states that  is fully faithful and we also get the left exactness very easily because
is fully faithful and we also get the left exactness very easily because 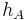 is already left exact. The proof of the right exactness is harder and can be read in Swan, Lecture notes on mathematics 76.
is already left exact. The proof of the right exactness is harder and can be read in Swan, Lecture notes on mathematics 76.
After that we prove that 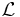 is abelian by using localization theory (also Swan).
is abelian by using localization theory (also Swan). 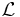 also has enough injective objects and a generator. This follows easily from
also has enough injective objects and a generator. This follows easily from 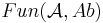 having these properties.
having these properties.
By taking the dual category of 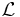 which we call
which we call 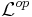 we get an exact and fully faithful embedding from our category
we get an exact and fully faithful embedding from our category 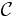 to an abelian category which has enough projective objects and a cogenerator.
to an abelian category which has enough projective objects and a cogenerator.
We can then construct a projective cogenerator  which leads us via
which leads us via 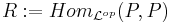 to the ring we need for the category of R-modules.
to the ring we need for the category of R-modules.
By 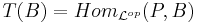 we get an exact and fully faithful embedding from
we get an exact and fully faithful embedding from 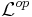 to the category of R-modules.
to the category of R-modules.
References
- R. G. Swan (1968). Lecture Notes in Mathematics 76. Springer.
- Peter Freyd (1964). Abelian categories. Harper and Row.
- Barry Mitchell (1964). The full imbedding theorem. The Johns Hopkins University Press.
- Charles A. Weibel (1993). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics.